wetchのブログ

他人に見られることを想定していない書き散らかし独習ノート．物理学とかVBAとか．

同型定理のイラスト

物理学・数学

ランキング参加中
知識

参考文献


以下，G, G' は群，H は部分群，N は正規部分群，e は単位元を表す．

準同型定理

定理 写像 f: G\rightarrow G' を準同型写像とする．このとき写像
\bar{f} : G/\operatorname{Ker}f\rightarrow G' : a\operatorname{Ker}f \mapsto f(a)
はwell-defined（代表元 a の取り方によらず定義される）で，単射準同型写像となる．したがって値域の方を狭めて
\bar{f} : G/\operatorname{Ker}f \rightarrow \operatorname{Im}f : a\operatorname{Ker}f \mapsto f(a)
と再定義すればこれは同型写像．すなわち G/\operatorname{Ker}f \simeq\operatorname{Im}f.

これのイラスト化を考えてみたのだけど，他の人が描いてる中では下の絵が一番分かりやすかった．


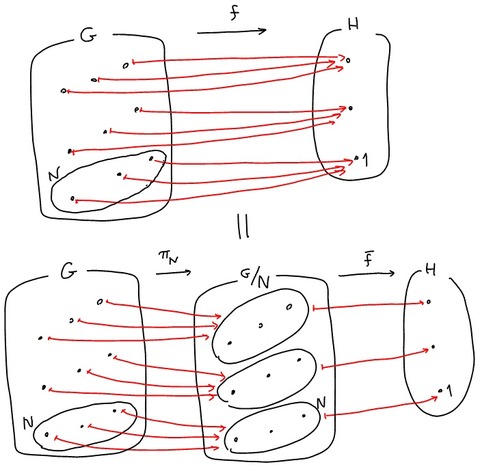
https://livedoor.blogimg.jp/rhideto/imgs/5/8/5809b1ce-s.jpg
rhidetoのblog : 例6. 剰余群と準同型定理

自分なりにも書いてみる．

まず G,G' とそれらをつなぐ写像 f がある．

G,G' とそれらをつなぐ写像 f がある

f は単射でないから f(k)=e' となる k\ne e もあり得るし，全射でないからどこからも矢印が飛んでこない c'\in G' も存在し得る．
全射じゃない部分は無視（\operatorname{Im}f \subset G' の部分だけを考慮）して，単射じゃない分は G の元を類別する（G/\operatorname{Ker}f を考える）ことで解消できる．

準同型定理のイラスト

そんなふうに \bar{f} を構成すると，この絵のように1対1対応がつけられる．

第1同型定理

準同型定理のことを第1同型定理と呼ぶことも多いようだけど，ここでは参考文献に倣ってそれとは異なる定理を挙げる．

定理 全射準同型写像 f:G\rightarrow G'， 正規部分群 N'\triangleleft G' とする．このとき N:=f^{-1}(N') \subset G は G の正規部分群であり，写像
g: G/N\rightarrow G'/N' : aN\mapsto f(a)N'
は同型写像となる．すなわち G/N \simeq G'/N'.

これは準同型定理において，G' の元を類別して（あるいは膨らませて）正規部分群による剰余群 G'/N' に置き換えるイメージ．
まず G,G',N' と f がこんな感じであって：

G,G',N'とf がこんな感じである

N' に対応する N:=f^{-1}(N') \subset G がこうなってて：

Nがこうなっている

G,G' を N,N' でそれぞれ割って G/N, G'/N' とすれば，この2つには1対1対応が付けられる．

第1同型定理のイラスト

第3同型定理

第1同型定理は群 G と別の群 G' のお話だったが，第2，第3同型定理では G' が出てこなくて，全部 G の中が舞台になっている．これはさっきまで G' として考えていたところを，同型性を利用して G の中に埋め込んでいる*1と考えることができる．

先に第3の方を説明しよう．第1同型定理を使うと第2より説明しやすい．

定理 N,M をともに G の正規部分群とし，N \subset M とする．このとき M/N は G/N の正規部分群であり，写像
f : G/N \rightarrow G/M : aN\mapsto aM
は全射準同型写像であって，写像
\bar{f}: G/M \rightarrow (G/N)\ /\ (M/N): aM \mapsto a(M/N)
は同型写像となる．すなわち G/M \simeq (G/N)\ /\ (G/M).

G/M, G/N, M/N を絵にしてとりあえず定理を絵にするとこんな感じか．

第3同型定理のイラスト

証明は準同型定理において \operatorname{Ker}f=M/N, \operatorname{Im}f=G/M とおくみたいな感じだが，第1同型定理からの導出のイメージとしては，まず第1同型定理の N を M に，N' を N に，G' を G/M に書き換えて，

N を M に，N' を N に，G' を G/M に書き換える．

で，G/M を G の中に埋め込むといった感じ．

G/M を G の中に埋め込む

第2同型定理

定理 部分群 H \subset G，正規部分群 N \subset G とする．このとき HN は G の部分群，H\cap N は H の正規部分群であり，写像
f : H/(H\cap N) \rightarrow HN/N : h(H\cap N) \mapsto hN
は同型写像となる．すなわち H/(H\cap N) \simeq HN/N.

イラスト化にあたっては HN と H\cap N をどう表すかというのが肝だろうと思う．検索すると下図のような感じの図がよくヒットする．


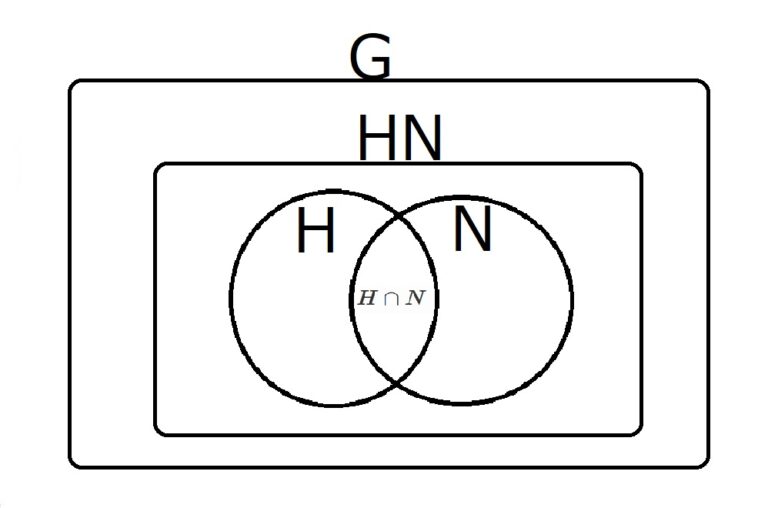
https://mathtano.com/wp-content/uploads/2023/08/isomorphism-theorems-2-768x508.jpg
第二同型定理を分かりやすく解説 | マスタノ！〜数学の楽しみ方〜

だが，乗積表のようなものを考えた方がより構造を表しうるんじゃないかと思う．

N と H の乗積表．注意：N\cap H は e 以外にもある．また，ある積 n_i h_j と別の積 n_i' h_j' はダブっていることもある．

で，この絵から H/(H\cap N), HN/N を考えると，

第2同型定理のイラスト

と，こんな感じになって同型になっていることが分かる．あとは第3同型定理のときと同様にして H を HN の中に埋め込む．

参考

群以前の定理

準同型定理の本質というか，代数構造を省いたら結局こういうことらしい．

定理 集合 X,Yに対し，写像 f:X\rightarrow Yを使ってX の同値関係 x\sim x' \Leftrightarrow f(x)=f(x') を定める．このとき X/\sim は完全代表系と同一視できる．すなわち写像
\phi: X/\sim \ \rightarrow \operatorname{Im}f: C(x)\mapsto f(x)
は全単射で，その逆写像は
\phi^{-1}: \operatorname{Im}f\rightarrow X/\sim \ : y\mapsto f^{-1}(\{y\}).
ここで C(x):=\{x'\in X|x'\sim x\} は x を代表元とする同値類．

*1:埋め込み（写像）とは，部分群 H \subset G から元の群 Gへの写像 \imath : H\rightarrow G : h\mapsto h のこと（明らかに単射準同型写像）．念のためメモしておいた．