wetchのブログ

他人に見られることを想定していない書き散らかし独習ノート．物理学とかVBAとか．

電流と磁場，電磁誘導のイラスト

電磁気学

電磁場を説明するイラスト，というか落書きをもう少し考えてみた．

アンペールの法則

直線電流

Qクーロンの点電荷は電束を“Q”に比例するだけの“本”数，略して“Q本”伴っている，みたいな考え方はガウスの法則の説明としてよく知られている．

https://detail-infomation.com/wp-content/uploads/2020/05/電束とは-600x221.jpg*1

それに類似するように，Iアンペアの直線電流は磁場の面を伴っていて，その枚数はIに比例する枚数，略してI枚であると考える．
すると電流の周りを一周する閉曲線Cが貫く磁場の面の枚数も当然I枚である．これがアンペールの法則

\displaystyle \oint_\mathrm{C} H \cdot \mathrm{d}l = I
のイメージ．

たとえば閉曲線Cが電流を中心とする半径rの円周であるなら，C上で磁場は一定でCの長さが2\pi rということだから，磁場の面の線密度，すなわち磁場は

\displaystyle H=\frac{I}{2\pi r} \tag{1}
となる．
上の図を正面から見たところ．破線は閉曲線Cを表す．

蛇足だが，この磁場の面は磁位の等値面とは考えない．

円形電流

電流Iが半径rの円形電流の場合，それに伴う磁場は実際は無限遠方まで存在し，こんな感じになる：


だけど、簡略化して次の図のように考えてしまおう：
円形電流の断面図．rは円の半径．
電流が伴うj枚の磁場の面は半径と同じrの距離までしか届かない．すると円の中心での磁場の強さが
\displaystyle H=\frac{I}{2r} \tag{2}

となることがイメージできるだろう．

「直線電流の式(1)には\piが付いて，円電流の式(2)には付かないので間違えないように覚えましょう」*2なんてこと言わないでも，この絵で理解するほうがわかりやすいと思う．

コイル

コイルの中の磁場はこんな感じになる：

コイルの断面図．茶色がコイルに流れる電流，橙色が磁場の面

  • 磁場の面はコイルの外部には出ない
  • 1本の電流は磁場の面をI枚伴う
  • その電流が1mあたりn巻きにされている

ということから

H=nI

がイメージできる．

電磁誘導

磁束線のループを1本考える（磁石か電磁石でもあったとする）．
磁石を動かすと磁束線の残像として電場が生じる．

磁束（茶色）のループが画面奥から手前への向きに動いているとき，電場（青）は磁束の残像として生じる．向きはレンツ則より決まる．
生じた電場がたまたま導線を横切れば，その導線の内部に電場が生じるわけだから電流が流れる．

*1:https://detail-infomation.com/electric-flux/

*2:たとえば直線電流、円形電流の作る磁場の公式 - どっちにπが入るか混ざるので... - Yahoo!知恵袋

偏微分の順序交換可能性って見た目で判別できないのか？

物理学・数学

2変数関数f(x,y)の偏微分の順序交換可能性，つまり

\displaystyle f_{xy} \equiv \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = f_{yx} \equiv \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)

とできるのはいつか？を考える．

別サイト*1を確認すると，3つの十分条件があって，前提条件の強い順に書くと

  • fがC^2級（全ての2階の偏導関数が存在して連続）ならよし．
  • f_{xy}とf_{yx}が存在していずれも連続ならよし．f_{xx}, f_{yy}の存在は仮定しない．
  • ​(SchwarzまたはClairaut) f_x, f_y, f_{xy}が存在して，f_{xy}が連続ならよし．f_{yx}の存在は後からついてくる．

というのがあるらしい．

たとえば

f(x,y) = \begin{cases} \dfrac{xy(x^2 - y^2)}{x^2+y^2} & \mbox{ for } (x, y) \ne (0, 0)\\ 0 & \mbox{ for } (x, y) = (0, 0) \end{cases}

が原点で順序交換不可能ということだが．．．
これってグラフの見た目では判別できないのか？
googleに書かせてみたグラフがこんな感じなんだが．

普通に滑らかな関数にしか見えない．
だとしたら今まで、「まあ多分交換可能だろ」と思って外微分を2回かけたらゼロにしてたけど，意外とそうとは言えない場合も多いかもしれない気がしてきて心配になってきた．

いや，物理ではこういうのをあまりうるさく言わない流儀なのは分かってはいるんだけど．

*1:偏微分の順序交換の十分条件とその証明 | 高校数学の美しい物語,
ヤングの定理 - Wikipedia

マクスウェル方程式，および電磁場の時間反転・空間反転のイラスト

電磁気学

wetch.hatenablog.com
wetch.hatenablog.com

やりたいこと

以前やったときと同じ．

  • 時間反転と空間反転を区別するのではなく，時空反転として統一的に記述したい．
  • 各変数ごとにマイナスが付くのかつかないのか思い出すのが大変なので，覚えやすい法則にしたい．

今回は「覚えやすい」の部分をより改善するため，絵にできないか試してみる．

Source field

電流，磁場

xy平面上にループ状の電流jが微小時間\Delta tだけ流れたとする．その瞬間だけ磁場（z成分H_zだけ）が生じる．この様子を絵にするとこんな感じ．


縦方向の座標軸を時間にしていることと，磁場H_zの向きを上向きの矢印でなく電流と同じ向きに回転する矢印で表していることに注意．
この絵でx=0の面に鏡を置いて，x方向について系を反転する．以前やったやつの成分の変換則より符号が変わるのはj_x \overset{x}\mapsto -j_x, H_z \overset{x}\mapsto -H_zで，j_yはそのままだから，そうなるよう向きを書き込むと

のようになる．Hを回転矢印で表したことで，軸性ベクトルだから云々，なんてことを考えなくても，自然に系を鏡に映した状態になっていることが分かる．
y軸について反転させても同様（符号が変わるのはj_y \overset{y}\mapsto -j_y, H_z \overset{y}\mapsto -H_z）：

時間軸方向に反転させると，電流jと磁場Hは時間反転で符号が変わらないから

となる．これもあたかもt=0面に鏡を置いて系を鏡映しにしただけと考えて違和感がない絵になっている．

電荷

ここでループ電流に電流が分断される箇所を入れる（コンデンサをイメージすればいい）．これで同様に時刻t_1に\Delta tだけ電流jを流すと，コンデンサの両極には\pm\rho=\pm j\Delta tの電荷が生じ，電流がなくなっても電荷は残り続ける．これは時間軸方向に伸びる線で電荷が表されることを意味する．少し後の時刻t_2にコンデンサを短絡させて電荷を消すとしよう．


時刻t_1,t_2の電流は，時間軸方向にずれているものの，合わせると閉ループになっている．この電流と自然につながるよう，電荷\pm\rhoを表す線に向きを付けよう．

すると上向きの線がプラスの，下向きのがマイナスの電荷を表すことになる．2本の電流の線および2本の電荷の線が合わさって時空内で閉ループになっている．
この絵をx, y, t軸方向にそれぞれ反転させる．電荷の符号が変わるのは時間反転のとき \rho \overset{t}\mapsto -\rhoだけだからそのように向きを書き込むと

となる．この絵でもそれぞの反転は自然な鏡映しで考えればいいことが分かる．

電束

電荷が存在するなら電束が生じるから，この絵にさらに電束を書き加えよう．この絵ではほぼD_xだけなのでそれだけ考えよう．D_xはプラスからマイナスの向きだが，この向きをHのような回転矢印で表して書き込む．


そして反転．D_xが符号変化するパターンはx軸反転とt軸反転のときD_x \overset{x\text{ or }t}\mapsto -D_xだから

となる．これでも成分の変換則と自然な鏡映しが整合している．いい感じだ．

Force field

磁場，ベクトルポテンシャル

絵を変えよう．x軸に沿った小さいコイルがあり，そこには過去からずっと電流が流れていて磁束Bが存在したとする．zx平面上の1本の磁束に注目すると，それはコイルを貫通する閉曲線になっている．そのBの内側にはベクトルポテンシャルAも存在する．Bがzx平面上にあることからAの成分はほぼA_yのみなのでそれだけ考えよう．状況を絵にするとこんな感じ．

縦方向の軸がtではなくzなのに注意．
この磁束Bをxy平面に平行な面で半分に切断してその断面だけを取り出し，縦方向の軸をzからtに変えて絵にする．断面では磁束はB_zだけが見えることになるが，それを回転矢印で表す．時間的にずっと存在していることも加えて絵にすると

となる．
この系をまずx軸で反転すると，符号変化するのはB_z \overset{x}\mapsto -B_zだけなのでそのように向きを書き込むと

となる．
同様にy, t軸で反転すると，符号変化するのはy軸反転のときのB_z \overset{y}\mapsto -B_z, A_y \overset{y}\mapsto -A_yだけなのでそのように向きを書き込むと

となる．やはりこの場合も自然に鏡映しにした状態と整合している．

電場

この系がある時刻でy方向に（一瞬で）移動し，また静止したとする．磁場が動いたので電場E_xができる．E_xの向きはこの絵だと外向き，広がるような向きだが，磁束と同じ向きの回転矢印で表す．


x, y, t軸反転で符号が変わるのはx軸反転とt軸反転 E_x \overset{x\text{ or }t}\mapsto -E_x なので絵にすると

となる．

スカラーポテンシャル

電場があるならスカラーポテンシャル\phiがあってもいい．Aと向きが合うよう矢印を書き込んでおく．反転で符号変化するのは\phi \overset{t}\mapsto -\phiであるので，いきなりx, y, t反転の図まで書くと


となる．

ちょっと待てよ．．．

ポテンシャルは4次元ベクトルでA^\mu=(-\phi,A_x,A_y,A_z)とか，4次元微分形式で-\phi\mathrm{d}t+A_i\mathrm{d}x^i}とか，[tex:\phiにはマイナスを付けてるんだよな．
ということは上の絵でも\phiだけ逆向きにするとか，そういうことを考えないといけないのではないのか？
まだちょっと整理できてない．

まとめ

電磁場の時間反転・空間反転による成分の変換則は，数式で考察しなくても，自然に絵をかけば直感的に理解できそうだ．擬ベクトルかどうかも関係ない．*1
ただし絵を描くルールとして，

  • 電荷\rhoとスカラーポテンシャル\phiの正負は時間軸方向を向く真っすぐな矢印の向きに変換する
  • 磁場H，磁束密度Bの向きは空間軸方向だけを含む面内で回転する矢印で表す
  • 電場E，電束密度Dの向きは時間軸方向を含めた面内で回転する矢印で表す

というのを考えなきゃいけないが．

参考

*1:実は関係ないこともない．\rho,j,H,Dの向きはホッジスターをとった状態で今回の絵では表しており，本来の擬ベクトル等の状態とはちょっと違う．

電磁場の図形的表現

電磁気学

過去の自分への進捗報告
wetch.hatenablog.com

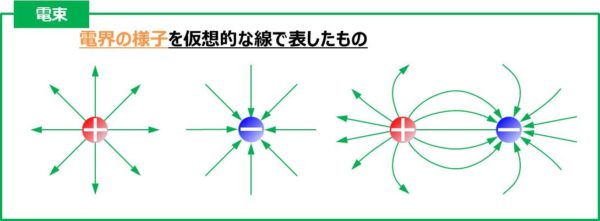
「『電磁場は微分形式で表現できる』∩『微分形式は図形的な解釈ができる』
　⇒『電磁場を図形的に表現できる』」

注意

  • 従来の矢印ベクトルで表す方法と比較して，今回の図形的表現の特徴は
    • メリットは，「右ねじの法則」あるいは「右手・左手の法則」というまったく直観的でない法則をほぼ排除できること．磁荷や磁極を考えない限りは大丈夫と思う．
    • デメリットは定量的な計算に不向きなこと．特に回転矢印を3次元数ベクトルに結び付けるのは難しいだろう．北野電磁気学 p.44も参照．
  • 光速は無限大．あるいは光速と比べて十分遅い範囲で考える．そのため，たとえば電束Dは電荷の動きに完全に（タイムラグなしに）追随して動く．

電荷密度\rho

小さな粒が粗密を付けながら空間に分布している様子をイメージする．それぞれの粒にはプラスかマイナスの符号が付いている．これはそんなに難しくないだろう．全く関係ない人様の画像を借りると下図のようなイメージか．


https://media.istockphoto.com/id/1277739137/ja/ベクター/円形の粒状の背景.jpg?s=612x612&w=0&k=20&c=W9MkdKloIyvE-Txji4gorqK7rx0ZZTttD3eeBttnI0w=*1

電流密度jと連続の式

電流は電荷の動きであるから，逆に電荷に注目して，電荷が動いた時の“残像”が電流であると捉える．プラス電荷の動きであればそれと同じ向きを電流は持つので，それを表すため矢印を添えておく．マイナス電荷であれば逆向き．このイメージと連続の式

\dot{\rho}+\operatorname{div}j=0
もしくは積分形
\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\int_V\rho\ \mathrm{d}V=-\int_{\partial V}j\cdot\mathrm{d}S
を対応付けて考えると，「方程式の中に時間微分が含まれているとき，時間微分されていない変数は“残像”を表す」という標語にすることができる．
https://previews.123rf.com/images/vectorpocket/vectorpocket2001/vectorpocket200100773/138371862-黒い背景に隔離青い火でサッカーボールを飛ぶ。火花とプラズマ炎の中でサッカーのベクトル現実的なシンボル。ポスター用テンプレート、スポーツ.jpg*2
ボールが電荷の，青く伸びる尾が電流のイメージ．（検索が悪いせいでそれっぽい画像を出せんかった．）

電束密度Dとガウスの法則

これも既存のイメージ通り，プラス電荷から発してマイナス電荷に集束する線のイメージでとらえる．これがガウスの法則

\displaystyle \operatorname{div}D=\rho,\quad\int_{\partial V}D\cdot\mathrm{d}S=\int_V\rho\ \mathrm{d}V
を表している．実際は1個の電荷は無数の電束とつながっているが，後述のことをイメージしやすくするために，電荷の個数と電束の本数は1：1になっていると考えておこう．電流のときは矢印の先がプラス電荷だったのに対し，電束の場合は逆に矢印の根元がプラス電荷になる．またこの式は時間微分を含まないので“残像”のイメージではないことに注意．

https://detail-infomation.com/wp-content/uploads/2020/05/電束とは-600x221.jpg*3

磁場Hとマクスウェル・アンペールの法則

電荷が動くときその残像として電流が生じると上述したが，電荷に引っ張られて電束も動くことになる．その残像が磁場である．

https://www.sci.u-toyama.ac.jp/topics/math/images/topicsJul2018_01.png*4
1本の電束が右奥から左手前へ移動するときにできる面が磁場のイメージ

磁場を電流との関係で考えよう．移動元にあった電荷の符号と電束の向きはもともとの逆になると考えると*5，移動元の電束，プラス電荷が動いた残像の電流，移動先の電束，およびマイナス電荷が動いた残像の電流の4本によって閉曲線が出来上がる．その内側に磁場を表す面ができる．磁場の向きは周囲の電流と電束の向きに合わせて回転する矢印で表す．これがマクスウェル・アンペールの法則
\displaystyle \operatorname{rot}H=j+\dot{D},\quad \int_{\partial S}H\cdot\mathrm{d}l = \int_S j\cdot\mathrm{d}S+\frac{\mathrm{d}}{\mathrm{d}t}\int_S D\cdot\mathrm{d}S
のイメージである．

スカラーポテンシャル\phi

これも既存イメージ通りでいいのだが，離散化した形で少しだけ手を加えておく．薄く色のついた半透明な物体を思い浮かべる．大きさの異なるその物体をいくつか持ってきて，空間内に重なるように配置していく．重なって色の濃くなった位置は\phiの値（絶対値）が大きいことを表す*6．
上述の標語に則って考えると，実はスカラーポテンシャルは残像である．

https://www.useful-python.com/wp-content/uploads/2022/12/contour_bwr.png*7

ベクトルポテンシャルAと磁束密度B

Aは空間内を埋め尽くす並行な*8曲面群*9に，向きを表す矢印を添えたものでイメージする．それらの曲面は縁を持つ場合があり，その縁のことを磁束Bという．Bの向きはAと合うようにする．これが

\displaystyle \operatorname{rot}A=B, \quad\int_{\partial S}A\cdot\mathrm{d}l=\int_S B\ \mathrm{d}S
のイメージである．
https://chie-pctr.c.yimg.jp/dk/iwiz-chie/ans-563397591?w=200&h=200&up=0*10
下側の，縁を持つ曲面Sがベクトルポテンシャルの，その縁\partial Sが磁束のイメージ

電場Eとファラデーの法則

静電場であれば電場は\phiの等値面，すなわち\phiの説明のとき登場した半透明の物体の表面であるとイメージすればよい．この場合Eは閉曲面になる．
動きがある場合．電場は磁束の“残像”である，つまり磁束の線が動けば残像として面ができ，その面が電場であるということが言える．これがファラデーの法則

\displaystyle \operatorname{rot}E+\dot{B}=0,\quad \int_{\partial S}E\cdot\mathrm{d}l+\frac{\mathrm{d}}{\mathrm{d}t}\int_S B\ \mathrm{d}S=0
だが，第2式はAを使って
\displaystyle \int_{\partial S}E\cdot\mathrm{d}l=-\int_{\partial S}\dot{A}\cdot\mathrm{d}l
とも書けることから別のイメージ：Aの面が動いた時にその“動いた部分”が電場であるというイメージでもいい*11．

構成方程式

“面”である電場や磁場と，“線”である電束や磁束を結びつけるのが構成方程式．簡単な比例関係

D=\epsilon E, H=B/\mu
で表されることが多いので結局同じものと勘違いされることもあるようだけど，非線形な場合とかテンソルの式になったりすることもあるのだから，正確には
D=D(E), H=H(B)
のように一般的な関数関係にあるとしか言えない．そしてこの関数関係は“面”と“線”を入れ替えるという幾何学的な役割を持っている．

クーロン力，ローレンツ力

力は微分形式で表しにくいので従来通りの矢印ベクトルのイメージで考える．
\phiの境界面（すなわちE）に\rhoが存在しているとき力が生じる．力の向きは\rho>0なら\mathrm{d}\phi<0の向き．
同様に，Aの境界（すなわちB）をjが通るときに力が生じる．ただし力の向きは逆で，\mathrm{d}Aがjと同じ向きを向くような向きにはたらく．

todo

  • 光速を有限値に落とし，電磁波のイメージをつかむこと．
  • 以前にやった，電磁波の時空間反転の考察をイラストにすること．
  • 4次元時空でのイメージを描くこと．これができれば電場と磁場が実は同じものを回転させただけということの意味が直観的にとらえられる．

*1:https://www.istockphoto.com/jp/イラスト/点描

*2:https://jp.123rf.com/photo_138371862_黒い背景に隔離青い火でサッカーボールを飛ぶ。火花とプラズマ炎の中でサッカーのベクトル現実的なシンボル。ポスター用テンプレート、スポーツ.html

*3:https://detail-infomation.com/electric-flux/

*4:https://www.sci.u-toyama.ac.jp/topics/math/201807.html

*5:もともとプラス電荷があって，それが動いた結果その位置での電荷がゼロになった場合，電荷の変化は\dot{\rho}=((0)-(+) )/\mathrm{d}t<0になる．

*6:符号は何か別の方法で区別できるものと考えておく

*7:https://www.useful-python.com/matplotlib-contour/

*8:互いに交わらないが，並行なら同じ位置に重なっていてもよい

*9:ミルフィーユ，本の断面，年輪，地層など，積層構造をもつ好きなものを思い浮かべればいい．

*10:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12234901857

*11:ただし向きは逆

共変微分とリー微分の比較

物理学・数学

共変微分\nabla_Xとリー微分L_Xのイメージがうまくつかめないので，とりあえず具体的な成分などを比較表にまとめておいて，今後考えていく予定．以下，

  • fはスカラー場，
  • X=X^i\ \partial/\partial x^i,\ Y=Y^i\ \partial/\partial x^iは反変ベクトル場，
  • \omega=\omega_i\ \mathrm{d}x^iは共変ベクトル場（微分1形式）．

また，反変ベクトル場と共変ベクトル場の内部積をi_X(\omega):=\omega_iX^iなどと書く．

共変微分 \nabla_X リー微分 L_X
日本語で定義を説明 ベクトルを別の点まで平行移動して差を取る ベクトルを別のベクトル場で流して差を取る*1
fに作用 \displaystyle \nabla_Xf=Xf=X^i\frac{\partial f}{\partial x^i} \displaystyle L_Xf=Xf=X^i\frac{\partial f}{\partial x^i}
Yに作用 \begin{align}&\nabla_XY\\&=X^j\left(\frac{\partial Y^i}{\partial x^j}\underline{+\Gamma_{jk}^iY^k}\right)\frac{\partial}{\partial x^i}\end{align} \begin{align}&L_XY=[X,Y]\\&=\left(X^j\frac{\partial Y^i}{\partial x^j}\underline{-Y^j\frac{\partial X^i}{\partial x^j}}\right)\frac{\partial}{\partial x^i}\end{align}
\omegaに作用 \begin{align}&\nabla_X\omega\\&=X^j\left(\frac{\partial\omega_i}{\partial x^j}\underline{-\Gamma_{ij}^k\omega_k}\right)\mathrm{d}x^i\end{align} \begin{align}& L_X\omega=(i_X\mathrm{d}+\mathrm{d}i_X)\omega\\&=\left(X^j\frac{\partial\omega_i}{\partial x^j}\underline{+\omega_j\frac{\partial X^j}{\partial x^i}}\right)\mathrm{d} x^i\end{align}
線形性 \begin{align}&\nabla_{X_1+X_2}Y=(\nabla_{X_1}+\nabla_{X_2})Y,\\&\nabla_X(Y_1+Y_2)=\nabla_XY_1+\nabla_XY_2,\\&\underline{\nabla_{fX}Y=f\nabla_XY}\end{align} \begin{align}&L_{X_1+X_2}Y=(L_{X_1}+L_{X_2})Y,\\&L_X(Y_1+Y_2)=L_XY_1+L_XY_2\end{align}
ライプニッツ \begin{align}&\nabla_X(fY)=(Xf+f\nabla_X)Y,\\&\underline{X\langle\omega,Y\rangle}\\&\underline{=\langle\nabla_X\omega,Y\rangle+\langle\omega,\nabla_XY\rangle}\end{align} \begin{align}&\underline{L_{(fX)}\omega=(fL_X+\mathrm{d}f\wedge i_X)\omega},\\&L_X(fY)=(Xf+fL_X)Y,\\&L_X(\omega_1\wedge\omega_2)\\&=(L_X\omega_1)\wedge\omega_2+\omega_1\wedge(L_X\omega_2)\\&L_X(\omega X)=...\end{align}
計量に 依存 独立
添字上げ下げ操作と 可換(テンソルになってる) 非可換?
外積\mathrm{d}との可換性 ? 可換

また，共変微分以外について，菅野，微分形式による解析力学，p.15によれば，k形式\omegaに対し

\displaystyle \begin{align} (\mathrm{d}\omega)(X_1,\dots,X_{k+1}) =&\ \sum_{i=1}^{k+1}(-1)^{i+1}X_i\left(\omega(X_iを除くX_1,\dots,X_{k+1})\right)\\ &+ \sum_{i\lt j}(-1)^{i+j}\omega\left([X_i,X_j],(X_i,X_jを除くX_1,\dots,X_{k+1})\right),\\ (L_X\omega)(X_1,\dots,X_k) =&\ X(\omega(X_1,\dots,X_k))\\ &- \sum_{i=1}^{k}\omega(X_1,\dots,[X,X_i],\dots,X_k),\\ (i_X\omega)(X_1,\dots,X_{k-1}) =&\ \omega(X,X_1,\dots,X_{k-1}).\end{align}

*1:お気持ちでふんわり理解するLie微分と共変微分｜あざらし

減衰振動と拡大配位空間

解析力学

減衰振動で遊ぶ．遊ぶだけなので新しい知見など期待しないこと．

参考文献

普通の配位空間

ラグランジュ形式\{x,\dot{x},t\}

Wikipediaに載ってたラグランジアンから始める：*1

\displaystyle L(x,\dot{x},t)=\frac{m}{2}(\dot{x}^2-\omega^2x^2)e^{2\gamma t}\quad \sim[\mathrm{J}].\tag{1.1}

ここで定数パラメータ\omega\sim[\mathrm{s}^{-1}]は固有角振動数，\gamma\sim[\mathrm{s}^{-1}]は減衰の強さを表している．

ここから運動量は

\displaystyle p:=\frac{\partial L}{\partial \dot{x}}=m\dot{x}e^{2\gamma t}\quad\sim[\mathrm{kg\ m/s}].\tag{1.2}

運動方程式は
\begin{align} 0 &= \dot{p}-\frac{\partial L}{\partial x}\\ \therefore\quad 0&= \ddot{x}+2\gamma\dot{x} + \omega^2x\end{align}\tag{1.3}

と分かる．

エネルギー収支式： v:=\dot{x}として運動方程式(1.3)の両辺にmvをかけると

\begin{align} 0&=mv\dot{v}+2m\gamma v^2+m\omega^2x\dot{x}\\ &=\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{m}{2}v^2+\frac{m}{2}\omega^2x^2\right)+2m\gamma v^2 \quad\sim[\mathrm{J/s}].\end{align}

よってK:=mv^2/2,\ U:=m\omega^2x^2/2\sim[\mathrm{J}]とすれば \displaystyle \frac{\mathrm{d}}{\mathrm{d}t}(K+U)=-4\gamma K \quad\sim[\mathrm{J/s}].\tag{1.4}
これは左辺が全エネルギー変化，右辺がエネルギーの減衰となり式全体としてはエネルギー収支を表す．

ハミルトン形式\{x,p,t\}

ハミルトニアンは

\begin{align} H(x,p,t)&:=p\dot{x}-L\\ &=\frac{p^2}{2m}e^{-2\gamma t}+\frac{m}{2}\omega^2x^2e^{2\gamma t} \quad\sim[\mathrm{J}].\end{align}\tag{1.5}

正準方程式は

\begin{align} \dot{p}&=-\frac{\partial H}{\partial x}=-m\omega^2 xe^{2\gamma t} \quad\sim[\mathrm{N}],\\ \dot{x}&=\frac{\partial H}{\partial p}=\frac{p}{m}e^{-2\gamma t} \quad\sim[\mathrm{m/s}],\\ \therefore\quad \ddot{x}&=-\omega^2 x - 2\gamma \dot{x}.\tag{1.6} \end{align}

運動方程式(1.3)が当然出てくる．

（以下，未完成）微分形式

作用積分Sの積分する前の量が，最小作用の原理よりゼロなので

0=\delta S=L\mathrm{d}t=p\mathrm{d}x-H\mathrm{d}t.

これを微分すると
\begin{align}0 &=\mathrm{d}L\wedge\mathrm{d}t\\ &=\mathrm{d}p\wedge\mathrm{d}x-\mathrm{d}H\wedge\mathrm{d}t\\ &=\left(\mathrm{d}p-\frac{\partial L}{\partial x}\mathrm{d}t\right)\wedge(\mathrm{d}x-\dot{x}\mathrm{d}t) \end{align}

または
\begin{align}0 &=\mathrm{d}p\wedge\mathrm{d}x - \mathrm{d}H\wedge\mathrm{d}t\\ &=\left(\mathrm{d}p+\frac{\partial H}{\partial x}\mathrm{d}t\right)\wedge\left(\mathrm{d}x-\frac{\partial H}{\partial p}\mathrm{d}t\right) \end{align}

正準変換

ハミルトン形式\{X,P,t\}

母関数

W(x,P,t):=xPe^{\gamma t} \quad\sim[\mathrm{Js}]\tag{2.1}

を使って正準変換する．位置と運動量は
\begin{align} X&=\frac{\partial W}{\partial P}=xe^{\gamma t} \quad\sim[\mathrm{m}],\\ p&=\frac{\partial W}{\partial x}=Pe^{\gamma t} \quad\sim[\mathrm{kg\ m/s}],\end{align}\tag{2.2}

またハミルトニアンは
\displaystyle K(X,P) = \frac{P^2}{2m}+\frac{m}{2}\omega^2X^2+\gamma XP\quad\sim[\mathrm{J}] \tag{2.3}

と変換される．

正準方程式は

\begin{align} \dot{P}&=-\frac{\partial K}{\partial X}=-m\omega^2 X-\gamma P \quad\sim[\mathrm{N}],\\ \dot{X}&=\frac{\partial K}{\partial P}=\frac{p}{m}+\gamma X \quad\sim[\mathrm{m/s}],\\ \therefore\quad \ddot{X}&=-(\omega^2 -\gamma^2) X \tag{2.4} \end{align}

と単振動になる．

ラグランジュ形式\{X,\dot{X},t\}

ハミルトニアンを逆ルジャンドル変換してラグランジアンにすると

\displaystyle L(X,\dot{X},t)=\frac{m}{2}\left\{\dot{X}^2-2\gamma X\dot{X}-(\omega^2-\gamma^2)X^2\right\}\quad\sim[\mathrm{J}].\tag{2.5}

∵Pと\dot{X}の関係を調べると
\begin{align} \dot{X}&=\frac{\partial K}{\partial P}=\frac{P}{m}+\gamma X,\\\therefore\quad P&=m(\dot{X}-\gamma X)\end{align}

だから
\begin{align}L(X,\dot{X},t) &=P\dot{X}-K\\ &=m(\dot{X}-\gamma X)\dot{X} - \frac{m^2(\dot{X}-\gamma X)^2}{2m}-\frac{m}{2}\omega^2X^2-m\gamma X(\dot{X}-\gamma X)\\ &=\frac{m}{2}\left\{\dot{X}^2-2\gamma X\dot{X}-(\omega^2-\gamma^2)X^2\right\}.\end{align}
■

逆にここから運動量を求めなおすと

\displaystyle P=m(\dot{X}-\gamma X) \quad\sim[\mathrm{kg\ m/s}].\tag{2.6}

運動方程式は

\begin{align}&\dot{P}-\frac{\partial L}{\partial X}=0,\\ \therefore\quad & \ddot{X}+(\omega^2-\gamma^2)X=0.\tag{2.7}\end{align}

拡大配位空間

ラグランジュ形式\{x,x',t,t'\}

tをxと同じく単なる運動の自由度であると見做し，新しい時間座標\tau\sim[\mathrm{\tau}]を使う*2*3．新しいラグランジアン \tilde{L} は作用積分が変わらない： \int L\mathrm{d}t=\int \tilde{L}\mathrm{d}\tau が成り立つように，

\begin{align}\tilde{L}(x,x',t,t')&:=t'L(x,\frac{x'}{t'},t)\\ &=t'\frac{m}{2}\left(\frac{x'^2}{t'^2}-\omega^2x^2\right)e^{2\gamma t}\quad \sim[\mathrm{Js/\tau}] \end{align}\tag{3.1}

と定義する．ここで\prime:=\mathrm{d}/\mathrm{d}\tau.

運動量はp_x,p_tの2成分になって

\begin{align} p_x&:=\frac{\partial \tilde{L}(x,x',t,t')}{\partial x'} = \left.\frac{\partial L(x,\dot{x},t)}{\partial \dot{x}}\right|_{\dot{x}=x'/t'}\\ &= m\frac{x'}{t'}e^{2\gamma t} & \sim[\mathrm{Ns}],\\ p_t&:=\frac{\partial \tilde{L}(x,x',t,t')}{\partial t'}\\ &= \left.L(x,\dot{x},t)-\frac{x'}{t'}\frac{\partial L(x,\dot{x},t)}{\partial \dot{x}}\right|_{\dot{x}=x'/t'} = -H\\ &= -\frac{m}{2}\left(\frac{x'^2}{t'^2}+\omega^2x^2\right)e^{2\gamma t} & \sim[\mathrm{J}]. \end{align}\tag{3.2}

運動方程式のx成分は

\begin{align} 0&=p_x'-\frac{\partial \tilde{L}(x,x',t,t')}{\partial x} = \left.t'\left(\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L(x,\dot{x},t)}{\partial \dot{x}}-\frac{\partial L(x,\dot{x},t)}{\partial x}\right)\right|_{\dot{x}=x'/t'}\\ &=m\left\{\left(\frac{x'}{t'}\right)' + 2\gamma\frac{x'}{t'}t' + \omega^2xt'\right\}e^{2\gamma t}, \\ \therefore\quad 0&=\frac{1}{t'}\left(\frac{x'}{t'}\right)'+2\gamma \left(\frac{x'}{t'}\right) + \omega^2x\\ &=\ddot{x} + 2\gamma\dot{x} + \omega^2x. \tag{3.3}\end{align}

上式にはx'/t'=\mathrm{d}x/\mathrm{d}t=\dot{x}を使った．これは運動方程式(1.3)に対応する．

t成分は

\begin{align} 0&=p_t'-\frac{\partial \tilde{L}(x,x',t,t')}{\partial t}\\ &= t'\left(\frac{\mathrm{d}}{\mathrm{d}t}(L(x,\dot{x},t)-\dot{x}p)-\frac{\partial L(x,\dot{x},t)}{\partial t}\right)\\ &=\frac{m}{2}\frac{\mathrm{d}t}{\mathrm{d}\tau}\left\{\frac{\mathrm{d}(\dot{x}^2)}{\mathrm{d}t} + 4\gamma \dot{x}^2 + \omega^2\frac{\mathrm{d}(x^2)}{\mathrm{d}t}\right\} \quad\sim[\mathrm{J/\tau}]. \end{align}\tag{3.4}

この式はK:=m\dot{x}^2/2, U:=m\omega^2x^2/2と置くと
\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}(K+U)=-4\gamma K \quad\sim[\mathrm{J/s}]

とエネルギー収支式(1.4)と同じになる．

ハミルトン形式\{x,p_x,t,p_t\}

ハミルトニアンを計算すると\tilde{H}=0になる．．．？

∵
\begin{align} \tilde{H}&:=p_xx'+p_tt'-\tilde{L}\\ &=m\frac{x'^2}{t'}e^{2\gamma t} - \frac{m}{2}\left(\frac{x'^2}{t'}+\omega^2x^2\right)e^{2\gamma t} - t'\frac{m}{2}\left\{\frac{x'^2}{t'^2}-\omega^2x^2\right\}e^{2\gamma t}\\ &=0.\quad \blacksquare\end{align}

ああそうか，これはゼロでいいんだ．\tilde Lはt',x'について1次同次なので，その両方でルジャンドル変換したらゼロになるんだ．熱力学で言うギブス・デュエムの式みたいなもんだ．

正準方程式は\tilde{H}=0より

\begin{align}p_x'&=0,& x'&=0,\\ p_t'&=0,& t'&=0\end{align}

になるように思うが，解としてt=\mathrm{const.}とか明らかにおかしいので，こういう場合（ラグランジアン\tilde{L}(x,x',t,t')がx',t'について1次同次で，\tilde{H}=0）は正準方程式を考えてはいけないのだろう．

（以下，未完成）

（ラウス形式\{x,x',t,p_t\}）
ルジャンドル変換をtだけ行うことにする．

\begin{align}\tilde{R}(x,x',t,p_t) &:=p_tt'-\tilde{L}\\ &=... \end{align}

で，xについてはラグランジュの運動方程式を，tについては正準方程式を考えてみる．
（以下未計算）

拡大配位空間を正準変換

ラグランジュ形式\{X,X',T,T'\}

母関数

W(x,t,P_X,P_T)=xP_Xe^{\gamma t}+tP_T \quad\sim[\mathrm{Js}]\tag{4.1}

を用いて\tilde{L}を
\begin{align} X=\frac{\partial W}{\partial P_X}&=xe^{\gamma t} &\sim[\mathrm{m}],\tag{4.2}\\ T=\frac{\partial W}{\partial P_T}&=t &\sim[\mathrm{s}],\tag{4.3}\\ p_x=\frac{\partial W}{\partial x}&=P_Xe^{\gamma t} &\sim[\mathrm{Js/m}], \tag{4.4}\\ p_t=\frac{\partial W}{\partial t}&=P_T+\gamma xP_Xe^{\gamma t} &\sim[\mathrm{J}] \tag{4.5} \end{align}

と正準変換すると*4
\begin{align}\tilde{L}(X,X',T,T') &=\frac{m}{2}T'\left\{\frac{X'^2}{T'^2}-2\gamma X\frac{X'}{T'}-(\omega^2-\gamma^2)X^2\right\}\\ &=T'L\left(X,\frac{X'}{T'},T\right) \quad\sim[\mathrm{Js/\tau}]. \end{align}\tag{4.6}

∵式(4.6)の\tilde{L}(X,T,X',T')に対して
\begin{align}X&=xe^{\gamma t},\\X'&=(x'+\gamma xt')e^{\gamma t},\\T'&=t'\end{align}

と変数変換すると式(3.1)と同じになること，および式(3.2)の運動量p_x, p_tの変換が
\begin{align} P_X=\frac{\partial \tilde{L}}{\partial X'}&=m\left(\frac{X'}{T'}-\gamma X\right)\\&=m\frac{x'}{t'}e^{\gamma t}=p_x e^{-\gamma t},\\ P_T=\frac{\partial \tilde{L}}{\partial T'}&=\frac{m}{2}\left(-\frac{X'^2}{T'^2}+(\gamma^2-\omega^2)X^2\right),\\&=\frac{m}{2}\left(-\frac{x'^2}{t'^2}-2\gamma x\frac{x'}{t'}-\omega^2x^2\right)e^{2\gamma t}=p_t-\gamma xp_x.　\end{align}

であること，これらを成立させる正準変換を試行錯誤で探すと式(4.1)のように母関数が見つかる．■

検算として，一般の正準変換で成り立つ

\mathrm{d}x\wedge\mathrm{d}p_x+\mathrm{d}t\wedge\mathrm{d}p_t=\mathrm{d}X\wedge\mathrm{d}P_X+\mathrm{d}T\wedge\mathrm{d}P_T \quad\sim[\mathrm{Js}] \tag{4.7}

がここでも成り立つことが確認できる．*5
∵式(4.2)-(4.5)を代入してばらせば
\begin{align} \mathrm{d}x\wedge\mathrm{d}p_x &=\mathrm{d}(Xe^{-\gamma T})\wedge\mathrm{d}(P_Xe^{\gamma T})\\ &=(e^{-\gamma T}\mathrm{d}X-\gamma Xe^{-\gamma T}\mathrm{d}T)\wedge(e^{\gamma T}\mathrm{d}P_X+\gamma P_Xe^{\gamma T}\mathrm{d}T)\\ &=\mathrm{d}X\wedge\mathrm{d}P_X+\gamma(P_X\mathrm{d}X+X\mathrm{d}P_X)\wedge\mathrm{d}T,\end{align}

\begin{align}\mathrm{d}t\wedge\mathrm{d}p_t &=\mathrm{d}T\wedge\mathrm{d}(P_T+\gamma (Xe^{-\gamma T})P_Xe^{\gamma T})\\ &=\mathrm{d}T\wedge\mathrm{d}P_T+\gamma \mathrm{d}T\wedge(P_X\mathrm{d}X+X\mathrm{d}P_X).\end{align}

この2式を足せばいい．■

運動量を\tilde{L}の微分でも求めておく．

\begin{align} P_X&=\frac{\partial \tilde{L}}{\partial X'}=m\left(\frac{X'}{T'}-\gamma X\right)=p_xe^{-\gamma t},\\ P_T&=\frac{\partial \tilde{L}}{\partial T'}=-\frac{m}{2}\left\{\frac{X'^2}{T'^2}+(\omega^2-\gamma^2)X^2\right\}=p_t-\gamma xp_x. \end{align}\tag{4.8}

この\tilde{L}を使うと運動方程式のx成分は

\displaystyle \frac{1}{T'}\left(\frac{X'}{T'}\right)'+(\omega^2-\gamma^2)X=0\tag{4.9}

で\tau微分をt微分に直せばこれは単振動の運動方程式(2.4), (2.7)である．
t成分は\partial\tilde{L}/\partial T=0より
\displaystyle 0=P_T'=-\frac{m}{2}\frac{\mathrm{d}}{\mathrm{d}\tau}\left\{\frac{X'^2}{T'^2}+(\omega^2-\gamma^2)X^2\right\}\tag{4.10}

という単振動のエネルギー保存則になる．

ハミルトン形式X,P_X,T,P_T

ハミルトニアン自体は正準変換前と同じくH=0.

正準変換後について，拡大後の運動量のT成分は，拡大前のハミルトニアン(2.3)になる：

P_T=-K(X,P_X).\tag{4.11}

∵式(4.4),(4.5)を変形していくと，
\begin{align}P_T &=p_t-\gamma x(p_x e^{-\gamma t})e^{\gamma t} & \text{from (4.4), (4.5)}\\ &=-\frac{m}{2}\left(\frac{x'^2}{t'^2}+\omega^2x^2\right)e^{2\gamma t}-\gamma x\left(m\frac{x'}{t'}e^{2\gamma t}\right) & \text{from (3.2)}\\ &=-\frac{m}{2}\left(\frac{x'^2}{t'^2}+2\gamma x\frac{x'}{t'}+\omega^2x^2\right)e^{2\gamma t}\\ &=-\frac{m}{2}\left(\dot{x}^2+2\gamma x\dot{x}+\omega^2x^2\right)e^{2\gamma t}\\ &=-\frac{1}{2m}(m\dot{x}e^{\gamma t})^2 - \gamma (xe^{\gamma t})(m\dot{x}e^{\gamma t}) - \frac{m}{2}\omega^2(xe^{\gamma t})^2\\ &=-\frac{1}{2m}(m\frac{x'}{t'}e^{\gamma t})^2 - \gamma X(m\frac{x'}{t'}e^{\gamma t}) - \frac{m}{2}\omega^2X^2 & \text{from (4.2)}\\ &=-\frac{P_X^2}{2m} - \gamma XP_X - \frac{m}{2}\omega^2X^2 & \text{from (3.2),(4.4)}\\ &=-K(X,P_X).\quad\blacksquare & \text{from (2.3)} \end{align}

Tに共役なP_TがTによらないことがすなわちP_Tが保存量であることを意味する，ってことでいいのかな？

（以下、未完成）

正準方程式は？
式(4.8)を微分して0と置く．

追記

山本，中村，解析力学2 (朝倉物理学大系)，p.531に拡大空間でのラグランジアンについての答えが書いてあって．
\tilde{H}=0というのはp_t+H(x,p,t)=0という拘束のある系を表すということだが．．．
しかし拘束系の扱いが難しすぎんか？

*1:\sim[\mathrm{J}]はこの式がエネルギーの次元を持つことを表す．以下同様に\simとSI単位で各式の次元を表す．検算の一助にするため．

*2:\tauは勝手に導入した変数なので明らかな次元を持たない．のでこう書くことにする．

*3:\tauという非物理的な量が気持ち悪い場合は，\tau微分が出てくる式に\mathrm{d}\tauをかけて，たとえばx'\mapsto\mathrm{d}x,t'\mapsto\mathrm{d}tという微分形式で考えればいいと思う．ただし2階微分の変形が難しくなるけど．

*4:配位空間を拡大してから正準変換するのと、正準変換してから配位空間を拡大するのが同じになることを一般的に示せるだろうか？

*5:\mathrm{d}\tilde{L}とも比較しておかないと．

ナビエストークス方程式と微分形式

参考


電磁気学は微分形式で表せてマクスウェルグリッドなるCAE手法ができるなら、流体力学も同じようにできるかもと思い調べてみたが、想像以上に難い。
流体のCFDにはすでに食い違い格子とかの概念はあるのだから、その基礎付けができると思ってはいるんだが。